【流体力学】【C++】圧縮性CFDの基礎

※この記事は「東京大学航空宇宙工学科／専攻 Advent Calendar 2018」用記事です．

-- 2020/11/2 修正 --
FVSのコードミスが発覚したため、結果を更新致しました。@ur_kinsk様、ご指摘頂きありがとうございます！

はじめに

自分は流体系の人間なので、今回も何か流体、特に数値流体の話がしたいなぁと思って考えてました。すると「あ、そういえば、空気力学第四でCFDやったけど、あれムズすぎてわからなかった気がする...　」ってなったので、今回は空気力学第四のパクリで圧縮性の話をしたいと思います。

Shock Captureの技術

圧縮性流体を考えるCFDの世界ではどのように衝撃波を捉えるかが重要になります。 CFD界隈では銀本と呼ばれる本（流体力学の数値計算法）を見ると、衝撃波捕獲法として重要な技法として二つあげています。

流束差分法（FDS）
流束分離法（FVS）

今回はその両方を紹介して、現在のCFD技術をちょこっと理解し~~た気になり~~ましょう！

一次元システム方程式

流体を少しでも齧ったことのある方ならきっとオイラー方程式くらいは知ってるはず。
今回の問題設定で考えるのは、そのオイラー方程式が使えるような状況、かつ一次元の衝撃波菅問題に関して考えたいと思います。流体の変数というのは基本的に以下の三つの保存則から定まります。

質量保存
運動量保存
エネルギー保存

当たり前といえば当たり前ですが、実はこの三つを完全に満たすようにCFDを作るのは基本的にはできないはずで、今回は触れないですが、精度とこれらの保存則は割とトレードオフの関係にあります。さて、ここで今回の問題で以上の保存則を表す方程式は以下の三つになります。

\begin{align} &\frac{\partial \rho}{\partial t} + \frac{\partial \rho u}{\partial x} = 0 \\ &\frac{\partial \rho u}{\partial t} + \frac{\partial (p + \rho^2 )}{\partial x} = 0 \\ &\frac{\partial e}{\partial t} + \frac{\partial(e+p)}{\partial x} = 0 \end{align}

ここで

\begin{equation} e = \frac{1}{2}\boldsymbol{v}^2 + e_{heat} \end{equation}

であるとして、 $e$ は流体のもつ全エネルギー、 $e_{heat}$ は流体の熱エネルギーであることに注意しましょう。この式、普段古典的な流体力学の授業で紹介されるような式の形をしていません。（例えば、参考 http://www.se.fukuoka-u.ac.jp/iwayama/teach/gfd/2007/chap3.pdf ）
もちろん、粘性がないからとか、 $e$ で全エネルギーを括ったからとかいうのはありますが、何より重要なのは、全て「時間微分項」＋「空間微分項」の形で表記されている点です。ゆえに、上の式は以下のように書き換えることが可能です。 \begin{equation} \label{qt} Q_t + E_x = 0 \end{equation} \begin{equation} \boldsymbol{Q} = \left( \begin{array}{c} \rho \\ \rho u \\ e \end{array} \right),\ \boldsymbol{E} = \left( \begin{array}{c} \rho u \\ p + \rho u^2 \\ (e+p)u \end{array} \right) \end{equation} つまり、これが「保存形」と呼ばれる流体のシステム方程式の形になります。確かにこれ、保存則の形そのまんまですしね。この式の上で、 $Q$ は「保存量」 $E$ は「流束」と呼ばれます。

ここで、式(\ref{qt})の形のままでは何もできません。すなわち、この式を局所的に線形化します（係数マトリックスを凍結するといいます）。

\begin{equation} \label{freeze} \frac{\partial Q}{\partial t} + A \frac{\partial Q}{\partial x}=0 \end{equation}

ただし、係数マトリックス $A\equiv \partial E/ \partial Q$ は $A_{ij} = \partial E_{ij} / \partial Q_{ij}$ のように計算できて、

\begin{equation} A = \left( \begin{array}{ccc} 0 & 1 & 0 \\ -\cfrac{3-\gamma}{2} u^2 & (3-\gamma u) & \gamma - 1 \\ \left(\cfrac{\gamma - 1}{2}u^2 - H \right)u & H - (\gamma - 1)u^2 & \gamma u \end{array} \right) \end{equation}

この $A$ を固有値分解すると次の三つの固有値を得ることができます。

\begin{align} \lambda_1 = u-c,&& \lambda_2 = u, && \lambda_3 = u+c \end{align}

ところで、式(\ref{freeze})を眺めると、これって輸送方程式 $u_t + cu_x = 0$ と同じ形であることがわかります。つまり、 $A$ が輸送速度に対応していると予測が立ちます。一般に $A$ は非対角成分を持ちますが、対角化することで独立な三つの波動方程式に分解でき、その三つの波の特性速度がこの行列の固有値として現れているのだと考えることができます。

実際、対角化は以下のように行われます。（後で使います） \begin{equation} A=R\Lambda R^{-1} \end{equation}

\begin{align} \boldsymbol{R} = \left( \begin{array}{ccc} 1 & 1 & 1 \\ u-c & u & u+c \\ H-uc& \cfrac{1}{2}u^2 & H+uc \end{array} \right),&& \boldsymbol{R}^{-1} = \left( \begin{array}{ccc} \cfrac{1}{2}\left(b_1 + \cfrac{u}{c}\right) & -\cfrac{1}{2}\left(\cfrac{1}{c} + b_2 u\right) & \cfrac{1}{2}b_2 \\ 1-b_1 & b_2u & -b_2 \\ \cfrac{1}{2}\left(b_1 - \cfrac{u}{c}\right) & \cfrac{1}{2}\left(\cfrac{1}{c} + b_2 u\right) & \cfrac{1}{2}b_2 \end{array} \right) \end{align}

なお、 \begin{align} b_1 = \frac{u^2}{2}\frac{\gamma - 1}{c^2}, && b_2 = \cfrac{\gamma - 1}{c^2} \end{align}

近似リーマン解法

CFDの基本的な手法として風上差分法というものが存在するのは知ってるでしょうか？風上差分法というのは、 \begin{equation} \frac{\partial u}{\partial x} = \frac{u_{n+1}-u_{n}}{\Delta x} \end{equation} のように移流項を風上側で差分をとって評価するもので、圧縮性の流体を考えるときには特に頻繁に使われます。なぜ中心差分法でも、後退差分法でもないのか？今回は詳しく説明しないですが、流れのもつ「情報」というものは基本的に「超音速」を超えた場合に風上からしか来ないからです。なぜなら、流れの情報というものは基本的に「音速」で伝達するものであり、流れが超音速を超えると、後ろからの情報は音速でしか伝わらないので、上流に伝播しなくなるからです。

さて、このような背景から今回は風上差分法を使います。ここまでをまとめるとこんな感じです。

オイラー方程式には三つの波が存在
情報は風上側から流れてくるので、風上差分法を用いるのが適切

さて、今までの話から、システム方程式の解法では三つの波が独立に存在し、それぞれに対して高解像度差分法を適用することが可能になります。 CFDの内部では次のグラフのような形でデータが存在しているとイメージしてください。

f:id:kane-please:20181205143345p:plain — CFDのイメージ

この次の時間ステップを求めるためには各セル境界面での流束を評価する必要があります。このように、二つの領域に渡って不連続な初期値をもつ双曲型の連立方程式を「リーマン問題」と呼びます。

f:id:kane-please:20181205151616p:plain — リーマン問題

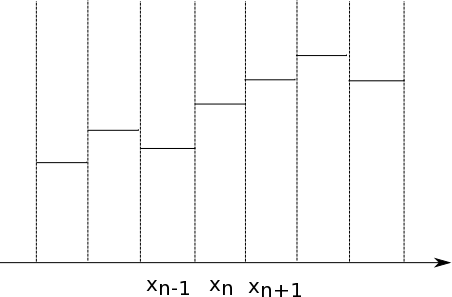
このリーマン問題の解から、セル境界面における通過する流束を求めることができる。この流束を $\tilde{E}_{j+1/2}$ とすると、

\begin{equation} \label{int} Q_j^{n+1}=Q_j^n - \frac{\Delta t}{\Delta x}(\tilde{E}_{j+1/2}^n - \tilde{E}_{j-1/2}^n) \end{equation}

として、次の時刻での保存量 $Q_j^{n+1}$ を求めることができる。この式から、各セルにおける物理量分布を求めることが可能になります。ところで、そもそもCFDの内部ではセル内で物理量が一定分布の近似したデータについて考えているので、その時点ですでに精度は失われており、わざわざ計算コストの高いリーマン問題を厳密に解く必要はありません。そこで、近似的にリーマン問題を満足するように $\tilde{E}_{j+1/2}^n$ を決めてしまえばいい。その近似手法の中でもよく知られた~~（古典的な）~~ものは以下の二つになります。

流束差分法（FDS）
流束分離法（FVS）

以下ではそれぞれの手法の説明をした後に、結果を比較したいと思います。

FDS (Flux Difference Splitting)

いわゆる「Roeスキーム」と呼ばれる手法になります。この手法の特徴としては、離散化されたデータからRoeの近似リーマン解を用いて出来るだけ物理的に正しい $j+1/2$ での数値流束を評価することで風上差分を行う、ということです。具体的に見てもらった方がわかりやすいかもしれないので、早速説明していきます。

Roeは非線形スカラー方程式に対する１次の風上差分を非線形のシステム方程式に拡張しました。このスキームでは１次精度の数値流束は以下の式で評価されます。

\begin{equation} \label{ffds} \tilde{E}_{j+1/2} = \frac{1}{2}(E_{j+1} + E_{j} -|A|_{j+1/2}(Q_{j+1} - Q_j)) \end{equation}

ただし、 \begin{equation} |A|_{j+1/2} = R_{j+1/2}|\Lambda|_{j+1/2}R_{j+1/2}^{-1} \end{equation}

ここで、添字の $j+1/2$ で表される量は以下のRoeの平均を用いて評価されます。また、ここでの絶対値 $|\cdot|$ の意味は全ての行列要素で絶対値をとる、という意味です。このRoeの平均というものはRoeが提案した線形分解によるリーマン解法であり、平均の値 $Q_{ave}$ が左右の状態 $Q_L, Q_R$ の非線形関数として定義されています。 \begin{align} \rho_{ave} &= \sqrt{\rho_L \rho_R}\\ u_{ave} &= \frac{\sqrt{\rho_L}u_L + \sqrt{\rho_R}u_R}{\sqrt{\rho_L} + \sqrt{\rho_R}}\\ H_{ave} &= \frac{\sqrt{\rho_L}H_L + \sqrt{\rho_R}H_R}{\sqrt{\rho_L} + \sqrt{\rho_R}}\\ c_{ave}^2 &= (\gamma - 1)\left(H_{ave} - \frac{1}{2}u_{ave}^2\right) \end{align}

FDSでの解析はまず式(\ref{ffds})により流束 $\tilde{E}_{j+1/2}$ を求めた後に式(\ref{int})に基づいて時間積分を行えば良いです。

式(\ref{ffds})の最後の項は数値粘性を表しており、証明は省略しますが、この項は物理量の「跳び」（例えば衝撃波付近は大きい）に対して数値粘性を付加しています。逆にいうと、「跳び」の少ない衝撃波から離れた領域に対しては数値粘性を付加しないので、正確になります。この点がFDSの優れている点です。

FVS (Flux Vector Splitting)

こちらは実際にはリーマン問題の近似解を実際に求めている訳ではないのですが、「スカラー方程式への風上差分をシステム方程式にも拡張している」という意味で~~なぜか~~近似リーマン解法に分類されています。この手法の特徴としては、「物理的な流束を各特性波の方向に応じて差分方向を切り替える」という点です。

考え方はとても簡単です。まず流束ベクトルを単純に $E^{+}(Q),E^{-}(Q)$ に分解します。ここで、 $E^+$ は左からくる正の固有値に対応する流束、 $E^-$ は右からくる負の固有値に対応する流束です。正の固有値を持つということは波（情報）が左からくるということなので後退差分を利用します。逆に負の固有値を持つならば波（情報）が右からくるということなので前進差分を利用します。それだけです。

それでは具体的に手法を見ましょう。流速の分解は実際には以下の式で行います。 \begin{equation} \Lambda^\pm = \frac{\Lambda \pm |\Lambda|}{2} \end{equation} $\Lambda^+$ は正の固有値を持つもののみから、 $\Lambda^-$ は負の固有値を持つもののみからなる。これより新しく以下のように $A^\pm$ が定義できます。 \begin{equation} A^\pm = R\Lambda^\pm R^{-1} \end{equation} さてこれらを用いて数値流束 $\tilde{E}_{j+1/2}$ を表示すると、 \begin{equation} \tilde{E}_{j+1/2} = E_{j+1/2}^+ (Q_{j+1/2}) + E_{j-1/2}^-(Q_{j+1/2}) \end{equation} 今回は一次精度の流束分離を行い、その時には次のように置くことができる。 \begin{align} Q_{j+1/2,L} = Q_j, && Q_{j+1/2,R} = Q_{j+1} \end{align} ここで、 $L, R$ はそれぞれ左からくる波、右からくる波に対応しています。つまり $E^+$ については、 $Q_L$ を、 $E^-$ については、 $Q_R$ をそれぞれ使用する必要がある。

よって数値流束 $\tilde{E}_{j+1/2}$ は次のように評価されます。 \begin{align} \tilde{E}_{j+1/2} &= E_{j+1/2}^+ + E_{j-1/2}^-\\ \label{ffvs} &= A_j^{+}Q_j + A_{j+1}^-Q_{j+1}\\ &= \frac{A_j + |A|_j}{2}Q_j + \frac{A_{j+1} + |A|_{j+1}}{2}Q_{j+1}\\ \label{flux_fvs} &= \frac{1}{2}(E_{j+1} + E_{j} -(|A|_{j+1}Q_{j+1} - |A|_{j}Q_j)) \end{align} あとはFDSの時と同様にして、式(\ref{ffvs})により流束 $\tilde{E}_{j+1/2}$ を求めた後に式(\ref{int})に基づいて時間積分を行うだけです。

さて、ここでFDSとFVSの違いに関して軽く述べると、式(\ref{ffds})と(\ref{flux_fvs})を見比べると、最後の項だけ違うことがわかります。
そもそも対流項 $\partial E/ \partial x$ の計算をしようとした時に、 $E_{j-1/2} - E_{j+1/2}$ をすることを考えると、最初の二項は二次精度中心差分を形成することがわかります。そして、残った最後の項が拡散項として働き、このスキームに風上差分のような特徴を加えていると考えることができます。（一般にCFDは中心二次精度差分は正確だが不安定、風上一時精度差分は安定だが鈍るのが特徴で、その両者の組み合わせをするのが差分スキームの基本です）
この拡散項がFDSでは必ず正になり、拡散を引き起こしますが、一方FVSではここが必ずしも正にはならないので、そこが本質的に異なっていると考えることができます。

実装

ここに示すと醜くなるので、Githubに置いておきました。見てみたい方はみてみるといいかもしれません。
ただ、適当にパパッと作ったので、クソコードなのは許してください。あと、Eigen使ってるので、そこだけ注意お願いします。

FDSのコード github.com
FVSのコード github.com
衝撃波管問題の解析解 github.com

結果

さて、それではFDSとFVSが実際の問題に適用した時にどのような挙動になるのか見てみましょう。今回は問題として、一次元の衝撃波管問題を考えました。 CFDの世界では衝撃波管問題が頻繁に用いられるのですが、その理由は

解析解がわかっているから
衝撃波、膨張波、接触面という圧縮性衝撃波で重要となる要素が全て含まれているからとして、頻繁にスキームのテスト問題として用いられます。

-- 2020/11/2 修正ここから --
以下の三つのグラフが解析解、FDS、 FVSの密度、速度、圧力の結果になります。

f:id:kane-please:20201102163849p:plain — 一次元衝撃波管問題の速度グラフ

f:id:kane-please:20201102164034p:plain — 一次元衝撃波管問題の圧力グラフ

f:id:kane-please:20201102164048p:plain — 一次元衝撃波管問題の圧力グラフ

さて、FDSはやはり特徴として衝撃波付近で鈍っていますね。これはそもそもスキームの段階で数値粘性がそのように働くよう作ったので狙い通りです。それでFVSはっと... うーん...FDSはまだそんなものかと思えますが、FVSの結果が異常に悪いですね...もしかしたら実装を間違えたかもしれないので、そこだけ申し訳ありません。

コードミスを修正した結果、FVSの方もFDSとかなり近い結果が得られています。やはり初期のFDS, FVSでは実用上では大きな違いがなかったように見られます。

一応、FVSは論文に衝撃波管問題への適用結果があったので、載せておきます。

f:id:kane-please:20181205191714p:plain — FVMの衝撃波管問題への適用結果（paperより）

いや、これも相当ひどいな（笑）今回私たちが学んだのは本当に最初のFVSです。このあと、FVSというジャンルの中には様々に新しいスキームが誕生しました。新しいスキームが出るってことは、この最初のFVSは使い物にならなかったからで、もしかしたら、自分の実装は間違ってなかったかもしれません（笑）

-- 2020/11/2 修正ここまで --

終わりに

どうですか？意外と圧縮性のCFDってそんなに難しくないんですよね。考え方はとても簡単なので皆さんに理解してもらえたなら幸いです。ところで、FDSとFVS、世界では今どちらが最も使われていると思いますか？ ...答えはFVSなんです！なんででしょうね？今圧縮性で頻繁に用いられているのはFVSから派生したAUSM系スキームと呼ばれるものです。（参考に入れておきます）最初はあんなに結果が悪くても、のちに誰かが発展させて広まっていくのは素晴らしいなぁと思いました。

誰か、自分の研究を代わりに発展させてくれないかなぁと思った今日この頃でした。

参考文献

基礎方程式の導出：http://center.stelab.nagoya-u.ac.jp/summer-school/pdf/text1-2.pdf
Steger, Joseph L., and R. F. Warming. "Flux vector splitting of the inviscid gasdynamic equations with application to finite-difference methods." Journal of computational physics 40.2 (1981): 263-293.
藤井孝造著：流体力学の数値計算法（東京大学出版会, 1994）
AUSM系スキーム：http://www.nagare.or.jp/download/noauth.html?d=34-2tokubetu2.pdf&dir=84